ಜೇನ ಲೆಕ್ಕ ಪಕ್ಕ

© ವಿಪಿನ್ ಬಾಳಿಗಾ
ಜೇನು ಎಂಬ ಶಬ್ಧವನಾಲಿಸಿದರೆ ಸಾಕು, ಜೇನು ತುಪ್ಪ ಜ್ಞಾಪಕಕ್ಕೆ ಬಂದು ಬಾಯಲ್ಲಿ ನೀರೂರುತ್ತದೆ. ಅದರಲ್ಲೂ ಕರಡಿ ಸೇವಿಸುವ ಹಲಸಿನ ಹಣ್ಣು ಮತ್ತು ಜೇನುತುಪ್ಪದ ಮಿಶ್ರಣ ಅದ್ಭುತ. ಹುಮ್…, ಅದು ಪಕ್ಕಕ್ಕಿರಲಿ ನಮಗೆಲ್ಲರಿಗೂ ತಿಳಿದಂತೆ ಜೇನು ಹೀರಿ ತರುವ ಮಕರಂದವ ಶೇಖರಿಸಿಡಲು ಒಂದು ಮನೆ ಬೇಕು. ಅದೇ! ಮನೆಯೆಂದರೆ ಗುಡಿಸಲು ಮನೆಯೋ, ಸೀಟಿನ ಮನೆಯೋ, ಹಂಚಿನ ಮನೆಯೋ ಅಥವಾ ಮಹಡಿ ಮನೆಯೋ ಎಂದು. ಓಹೋ.. ಎಲ್ಲಾ ಜೇನುಹುಳುಗಳು ಈ ರೀತಿ ಮನೆಕಟ್ಟಲು ಪ್ರಾರಂಭಿಸಿದರೆ ಮನುಷ್ಯರ ಮಾಳಿಗೆಗಳಿಗಿಂತ ಹೆಚ್ಚಿರುತ್ತಿದ್ದವೇನೋ….? ಮತ್ತೆ ಜಾಗಕ್ಕೂ ಎಲ್ಲಿಲ್ಲದ ಯುದ್ಧವು ಶರುವಾಗುತ್ತಿತ್ತೇನೋ? ಹೋಗ್ಲಿ ಬಿಡಿ. ಆ ಹುಳುಗಳಿಗೇನು ದುರಾಸೆಯಿಲ್ಲ, ನಿಮ್ಮ ಮನೆಯ ಒಂದು ಮೂಲೆಯೋ, ಬಂಡೆಯ ತುದಿಯೋ, ಗಿಡವೋ, ಮರವೋ-ಅಂತಹ ಜಾಗೃತ ಸ್ಥಳ ಸಾಕು ತನ್ನ ಮೇಣದಿಂದ ಮನೆಯ ನಿರ್ಮಿಸಿ ತನ್ನ ಜೀವ ಸಂಕುಲ ಬೆಳೆಸೋಕೆ.
ಮೇಣ ಎಂದಾಗ ಮೂಡುವ ಪ್ರಶ್ನೆ, ಮೇಣ ಎಲ್ಲಿ ಸಿಗುವುದು? ಹೇಗೆ ಕೊಂಡು ತರುವುದು? ಎಂದು. ವಿಶೇಷವೇನೆಂದರೆ, ತಾನು ಸೇವಿಸುವ ಜೇನು ತುಪ್ಪದ ಸಹಾಯದಿಂದ ಮೇಣವು ದೇಹದಿಂದಲೇ ಸ್ರವಿಸಲ್ಪಡುತ್ತದೆ. ಹೇಗಂತೀರ? ಜೇನು ಹುಳುಗಳು 8 0z (1 0z=28 grams) ನಷ್ಟು ಜೇನು ತುಪ್ಪ ಸೇವಿಸಿದರೆ 1 0z ನಷ್ಟು ಮೇಣ ಸ್ರವಿಸಲ್ಪಡುತ್ತದೆ. ಅಬ್ಬಾ…! ಎಷ್ಟು ವಿಸ್ಮಯ ಅಲ್ವೇನ್ರಿ…! ಅದಕ್ಕೆ ಅನ್ಸುತ್ತೆ ಜೇನು ಹುಳುಗಳು ಎಷ್ಟೇ ಕಷ್ಟವಾದರೂ ಸಾವಿರಾರು ಮೈಲಿ ಹಾರಿ ಹೀರಿ ಮಕರಂದವ ತರುವುದು. ಹಾಗೆ ತಂದ ಮಕರಂದದ ಶೇಖರಣೆಯು ಅಷ್ಟೇ ಮುಖ್ಯ. ಮೇಲೆ ನೋಡಿದ ಹಾಗೆ ಅವುಗಳ ಆಹಾರ, ಲಾರ್ವಗಳ ಪೋಷಣೆ ಮತ್ತು ಗೂಡಿನ ನಿರ್ಮಾಣಕ್ಕೆ ಜೇನು ತುಪ್ಪ ಅತ್ಯಮೂಲ್ಯ. ಹೌದು ಇದರೆಲ್ಲದರ ಬಾಳ್ವಿಕೆಯ ಗುಟ್ಟು ನಿರ್ಮಾಣಿಸಲ್ಪಡುವ ಗೂಡಿನಲ್ಲಿದೆ. ಹೇಗಂತೀರಾ? ಒಮ್ಮೆಯಾದರೂ ಗೂಡೀನಾಕೃತಿಯ ವೈಖರಿಯನ್ನು ಗಮನಿಸಿದ್ದೀರಾ? ಗಮನಿಸಿದಾಗ ತಿಳಿಯುತ್ತದೆ ಇಲ್ಲೂ ಕೂಡ ಗಣಿತಜ್ಞ ಇದ್ದಾನೆಂದು.
ಹೇಗೆಂದರೆ ಆ ಜೇನ ರಾಡೆಯಲ್ಲಿನ ಎಲ್ಲಾ ತೂತುಗಳು ಷಟ್ ಭುಜಾಕೃತಿಯಾಗಿವೆ (Hexagonal). ಇದ ಗಮನಿಸಿದೊಡನೆ ಮೂಡುವ ಪ್ರಶ್ನೆ ಏನೆಂದರೆ, ಏಕೆ ಷಟ್ ಭುಜಾಕೃತಿಯೇ ಆಗಬೇಕು? ಬೇರೆ ಆಕೃತಿಗಳು ಅಂದರೆ ವೃತ್ತ (Circle), ತ್ರಿಭುಜ (Triangle), ಚೌಕ (Square) ಅಥವಾ n-ನಿಯಮಿತ ಬಹುಭುಜಾಕೃತಿ (Regular Polygon) ಯಾಕಾಗಬಾರದು? ಎಂದು. ಮೊದಲೇ ತಿಳಿದಹಾಗೆ ಜೇನು ತನ್ನ ಹೆಚ್ಚು ಪ್ರಮಾಣದ ತುಪ್ಪ ಸೇವನೆಯಲ್ಲಿ ಅಲ್ಪ ಪ್ರಮಾಣದ ಮೇಣ ಸ್ರವಿಸುತ್ತದೆ. ಹೀಗಿರುವಾಗ ಆಕೃತಿಯ ಜೋಡಣೆಯಲ್ಲಿ ಜಾಗ ಉಳಿಸಿದರೆ ಆ ಹುಳುಗಳಿಗೆ ಉಪಯೋಗಕ್ಕಿಂತ ನಷ್ಟವೇ ಹೆಚ್ಚು.
ಇಲ್ಲಿ ನೋಡಿ, ಒಂದು ಸಣ್ಣ ವಿಶ್ಲೇಷಣೆ. ಈ ಮೇಲೆ ಹೇಳಿರುವಂತೆ ಎಲ್ಲಾ ಆಕೃತಿಗಳನ್ನು ಜೋಡಿಸೋಣ, ಆಗ ನಮಗೆ ತಿಳಿಯುತ್ತದೆ, ಯಾವ ಆಕೃತಿಯ ಗುಣವು ಹೇಗೆಂದು
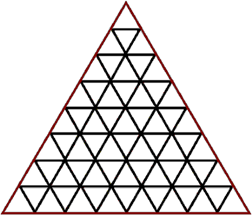

ಚೌಕ
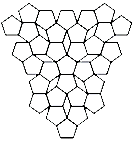
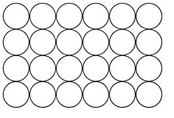
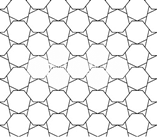


ಈ ಮೇಲಿನವುಗಳಲ್ಲಿ ತ್ರಿಭುಜ, ಚೌಕ ಮತ್ತು ಷಟ್ ಭುಜಾಕೃತಿಗಳಲ್ಲಿ ಮಾತ್ರ ಜಾಗ ವ್ಯರ್ಥವಾಗುತ್ತಿಲ್ಲ. ಆದರೆ ಇಲ್ಲಿ ಮೂರು ಆಕೃತಿಗಳು ಆ ಗುಣ ಹೊಂದಿರುವಾಗ ಷಟ್ ಭುಜಾಕೃತಿಯೆ ಯಾಕೆ? ಸಮಾಧಾನ… ನಮ್ಮ ಗಣಿತಜ್ಞರು (ಜೇನುಹುಳುಗಳು) ಅದಕ್ಕೂ ಕಾರಣವನ್ನು ಇಟ್ಟಿದ್ದಾರೆ. ಆ ಕಾರಣವನ್ನರಿಯಲು ನಾವು ಸ್ವಲ್ಪ ಲೆಕ್ಕಾಚಾರ ಮಾಡಬೇಕು. ಹಾಗೆ ಆ ಲೆಕ್ಕಾಚಾರದಿಂದೊದಗುವ ಸೂತ್ರವನ್ನು ಸರಿಯಾಗಿ ಅರ್ಥಮಾಡಿಕೊಂಡರೆ ಸಾಕು, ಇಲ್ಲಿ ನೋಡಿ.
ಮೊದಲು ಒಂದು ನಿಯಮಿತ ಷಟ್ ಭುಜಾಕೃತಿಯ ಭುಜದ ಅಳತೆ S ಎಂದು ಪರಿಗಣಿಸಿ.
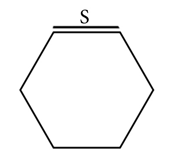
ನಂತರ, ಈ ಮೇಲಿನ ಆಕೃತಿಯನ್ನು ಆರು ಸಮನಾದ ತಿಭುಜಗಳನ್ನಾಗಿ ಕತ್ತರಿಸಿ.
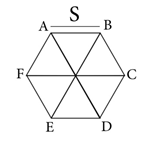
ಈ ಮೇಲಿನ ಆರು ತ್ರಿಭುಜಗಳಲ್ಲಿ, ಒಂದನ್ನು ತೆಗೆದುಕೊಂಡು ಅದರ ಮಧ್ಯ ಲಂಬ ಕೋನವಾಗಿ ಒಂದು ಉದ್ದನೆಯ ಗೆರೆ AB ಗೆ ಎಳೆಯಿರಿ.
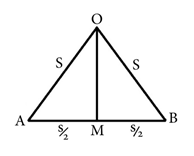
ಈಗ, ಭುಜ ಸರ್ವಸಮಾನತೆಯ (SSS congruence) ಉಪಯೋಗದಿಂದ ಎತ್ತರ (OM) ಕಂಡುಕೊಳ್ಳಬಹುದು. ಹೇಗೆಂದರೆ
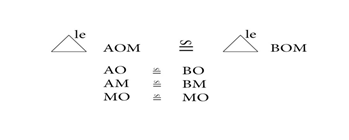
ಹಾಗೂ ಪೈಥಾಗೋರಸ್ [ಪ್ರಮೇಯದ ಪ್ರಕಾರ]
ತ್ರಿಭುಜ AOB, AO^2=AM^2 +OM^2
S^2 = S^2 / 4+OM^2
→OM^2 =S^2-S^2/4=3S^2/4
ಎತ್ತರ=OM=√3 S/2
ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣ= ½ x ಉದ್ದ x ಎತ್ತರ
= 1/2×S×√3 S/2
= √3 〖S^2/4〗
ಷಟ್ ಭುಜಾಕೃತಿಯ ವಿಸ್ತೀರ್ಣABCDEFA =6 [ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣ]
ಷಟ್ ಭುಜಾಕೃತಿಯ ಸುತ್ತಳತೆ =6S
ನಾವು ಮೊದಲೇ ಚರ್ಚಿಸಿದಂತೆ, ಈ ಮೂರರಲ್ಲಿ ಯಾವ ಷಟ್ ಭುಜಾಕೃತಿಯು ಉತ್ತಮವೆಂದು ಹೇಳಲು ಎಲ್ಲಾ ಮೂರು ಆಕೃತಿಗಳ ವಿಸ್ತೀರ್ಣ (Area) ಮತ್ತು ಸುತ್ತಳತೆಯ (Perimeters) ಅನುಪಾತ (Ratio) ಹೆಚ್ಚಿದ್ದಲ್ಲಿ. ಜೇನಿನ ಕಾರ್ಯದಕ್ಷತೆ ಹೆಚ್ಚಿರುತ್ತದೆ ಎಂದು.
| ಆಕೃತಿ | ವಿಸ್ತೀರ್ಣ(A) | ಸುತ್ತಳತೆ(P) | ಅನುಪಾತ(R=A/P) |
| ತ್ರಿಭುಜ | 〖√3 S〗^2/4 | 3 | √3 S/12 |
| ಷಟ್ಭುಜಾಕೃತಿ | S^2 | 4 | S/4 |
| ಚೌಕ | 3√3 S^2/2 | 6 | √3 S/4 |
ಇಲ್ಲಿ ಗಮನಿಸಿದೊಡೆ ತಿಳಿವುದು ಷಟ್ ಭುಜಾಕೃತಿಯ ಅನುಪಾತದಲ್ಲಿ ಯಾವ ಲೋಪದ ಆಲಾಪ ಮೂಡದಿರುವುದರಿಂದ ಇದರ ಆಯ್ಕೆಯನೊಪ್ಪುವುದರಲ್ಲಿ ಯಾವುದೇ ಸಂಶಯವಿಲ್ಲ, ಈ ಆಕೃತಿಯಿಂದ ನಿರ್ಮಾಣವಾದ ಯಾವುದೇ ವಸ್ತುವಿಗೆ ಬೀಳುವ ಒತ್ತಡವು ಸರಿಸಮಾನವಾಗಿ ಹಂಚಿಹೋಗುತ್ತದೆ. ಹಾಗೆ ಇಲ್ಲಿಯೂ ಕೂಡ ಜೇನುತುಪ್ಪದ ಒತ್ತಡವನ್ನು ಒಗ್ಗಿಸಿಕೊಳ್ಳುವ ಗುಟ್ಟು ಈ ಆಕೃತಿಯಲ್ಲಿದೆ ಎಂದು.
ಮುಂದೆ ನಾನೇನೂ ಹೇಳಲಾರೆ… ನಿಮ್ಮ ಪ್ರಶ್ನೆಗಳಿಗೆ ಉತ್ತರ ಕೊಟ್ಟಾಯಿತು. ಆದರೆ ನಾವು ಗಮನಿಸಿದಂತೆ ಅವುಗಳು ಆಹಾರ ಹುಡುಕುವ ಸಂಚಾರದಲ್ಲಿ, ಸಣ್ಣ ತನವಿಲ್ಲದ ಸಂಜ್ಞೆಯನ್ನು ಗಮನಿಸಬಹುದು, ಅವು ತಮಗೆಂದು ಆಹಾರ ಹುಡುಕುವ ಯತ್ನದಲ್ಲಿ ನಮಗೂ ಆಹಾರ ಸಿಗುವಂತೆ, ನೆರಳು ಸಿಗುವಂತೆ, ನೀರು, ಗಾಳಿ ಸಿಗುವಂತೆ, ಒಟ್ಟಾಗಿ ಇನ್ನೊಂದು ಜೀವಿಯ ಜೀವಕ್ಕೂ ಬೆಲೆಕೊಡುತ್ತವೆ. ಪರಾಗಸ್ಪರ್ಶದ (Pollination) ಮೂಲಕ. ಹೀಗಿರುವಾಗ ಅವುಗಳ ಉಳಿವು ನಮ್ಮ ಕೈಲಿಲ್ಲದಿದ್ದರು ನಾಶ ಮಾತ್ರ ನಮ್ಮಿಂದಾಗಬಾರದು.
ಲೇಖನ: ಗೀತಾ .ಆರ್
ಬೆಂಗಳೂರು ಜಿಲ್ಲೆ



